las integrales toman un puesto crucial en la rama de la física con el diagrama mostrado a continuación se puede plasmar el ciclo con respecto a las magnitudes físicas.
 |
| diagrama de flujo
CONCEPTO RESUMIDO DE CALCULO INTEGRAL
INTEGRALES APLICADAS A LA FÍSICA
|
ESPACIO RECORRIDO EN UN MOVIMIENTO RECTILÍNEO
Para un objeto con movimiento rectilíneo la función posición, s(t), y la función velocidad, v(t), se relacionan por s(t) = 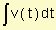 .
.
De este hecho y del teorema fundamental del cálculo se obtiene: 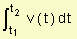 =
= 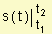 = s(t2) - s(t1)
= s(t2) - s(t1)

Un desplazamiento positivo significa que el objeto está más hacia la derecha en el instante t2 que en el instante t1, y un desplazamiento negativo significa que el objeto está más hacia la izquierda. En el caso en que v(t) ³ 0 en todo el intervalo de tiempo [t1, t2], el objeto se mueve en la dirección positiva solamente, de este modo el desplazamiento s(t2) - s(t1) es lo mismo que la distancia recorrida por el objeto.

En el caso en que v(t) £ 0 en todo el intervalo de tiempo, el objeto se mueve en la dirección negativa solamente, por tanto, el desplazamiento s(t2) - s(t1) es el negativo de la distancia recorrida por el objeto.
En el caso en que v(t) asuma valores tanto positivos como negativos durante el intervalo de tiempo [t1, t2], el objeto se mueve hacia adelante y hacia atrás y el desplazamiento es la distancia recorrida en la dirección positiva menos la distancia recorrida en la dirección negativa. Si quiere encontrarse la distancia total recorrida en este caso (distancia recorrida en la dirección positiva más la distancia recorrida en la dirección negativa) debe integrarse el valor absoluto de la función velocidad, es decir:
distancia total recorrida durante el intervalo de tiempo [t1, t2]
| = |
Un objeto se mueve con movimiento rectilíneo de modo tal que su velocidad en el instante t es v(t) = t2 - 2t metros por segundo. Halle:
a) el desplazamiento del objeto durante los tres primeros segundos.
b) la distancia recorrida durante ese tiempo.
a)  =
= 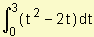 =
= 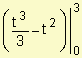 = 0.
= 0.
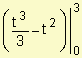 = 0.
= 0.
Esto significa que el objeto se encuentra en la misma posición en el instante t = 3 que en el instante t = 0.
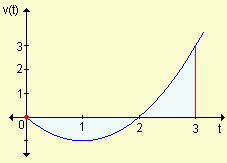
b) La velocidad puede escribirse como v(t) = t ( t - 2) de modo que v(t) ³ 0 si 2 £ t £ 3 y la velocidad es negativa si 0 £ t £ 2.
La distancia recorrida es:
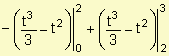 =
=
distancia recorrida = 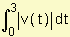 =
=  .
.
Podemos asegurar que la distancia recorrida es de  metros.
metros.
CINEMÁTICA
CONCEPTO DE TRABAJO
El trabajo que realiza una fuerza sobre un cuerpo equivale a la energía necesaria para desplazar este cuerpo. El trabajo se conoce como una magnitud física escalar que se representa con la letra W (del
inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el sistema internacional de unidades.
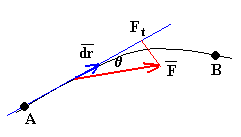
Donde Ft es la componente de la fuerza a lo largo del desplazamiento, ds es el módulo del vector desplazamiento dr, y q el ángulo que forma el vector fuerza con el vector desplazamiento.
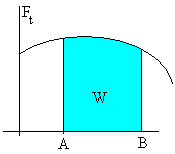
El trabajo total a lo largo de la trayectoria entre los puntos A y B es la suma de todos los trabajos infinitesimales
|
Ejemplo:
Calcular el trabajo necesario para estirar un muelle 5 cm, si la constante del muelle es 1000 N/m.
La fuerza necesaria para deformar un muelle es F=1000·x N, donde x es la deformación. El trabajo de esta fuerza se calcula mediante la integral
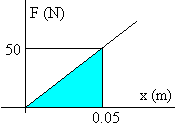 | 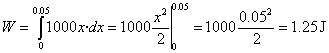
El área del triángulo de la figura es (0.05·50)/2=1.25 J
|
W=Ft·s
TRABAJO REALIZADO POR UNA FUERZA CONSTANTE
Si un objeto se mueve una distancia d en la dirección de una fuerza constante F aplicada sobre él, entonces el trabajo w realizado por la fuerza se define como w = F . d
Existen muchos tipos de fuerzas: centrífuga, gravitacional, etc. Una fuerza cambia el estado de reposo o de movimiento de un cuerpo. Para las fuerzas gravitacionales en la tierra se suelen utilizar unidades de medida correspondientes al peso de un objeto.
Cuando la fuerza es constante todo parece sencillo pero cuando se aplica una fuerza variable a un objeto se necesita el cálculo para determinar el trabajo realizado ya que la fuerza varía según el objeto cambia de posición.
Ejemplo:
Calcular el trabajo de una fuerza constante de 12 N, cuyo punto de aplicación se traslada 7 m, si el ángulo entre las direcciones de la fuerza y del desplazamiento son 0º, 60º, 90º, 135º, 180º.
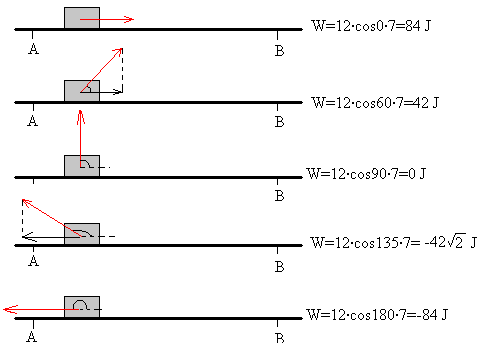
- Si la fuerza y el desplazamiento tienen el mismo sentido, el trabajo es positivo
- Si la fuerza y el desplazamiento tienen sentidos contrarios, el trabajo es negativo
- Si la fuerza es perpendicular al desplazamiento, el trabajo es nulo.
BIBLIOGRAFIA
-http://es.wikipedia.org/wiki/Cinem%C3%A1tica
-http://es.wikipedia.org/wiki/Trabajo_(f%C3%ADsica)
-http://www.fca.unl.edu.ar/Intdef/AplicacionesFisica.htm
-http://www.sc.ehu.es/sbweb/fisica/dinamica/trabajo/energia/energia.htm
